BTS : lettre de rentrée 2023 de l’inspection générale
La lettre de rentrée de l’inspection générale de l’éducation, du sport et de la recherche de mathématiques fait notamment le point sur les rénovations de filières et l’évolution des modalités de certification. Pour la télécharger ainsi que les modules du programme de...
Lettre de la rentrée 2023 à destination des professeurs de mathématiques physique-chimie de l’académie de Nice https://www.pedagogie.ac-nice.fr/plpms/wp-content/uploads/sites/19/2023/10/lettre_2023_2024_MSLP.pdf
Réforme des lycées professionnels
La réforme des lycées professionnels se déploiera progressivement à partir de la rentrée scolaire 2023. Douze grandes mesures ont été décidées qui visent à : Lutter contre le décrochage scolaire ; Améliorer la réussite dans les poursuites d’études ; Améliorer...
Définition de l’épreuve de mathématiques de Brevet Professionnel
L’arrêté du 23 avril 2023 modifie la définition de l’épreuve de mathématiques de BP. Les principales évolutions de la définition de cette épreuve : mise en cohérence avec le préambule et les contenus du programme de mathématiques (algorithmique…) ; plus grande...
Conférence sur les mathématiques
Deux Conférences exceptionnelles de Tadashi Tokieda 2 mai à Nice / 3 mai à Sophia Maths pures comme physique appliquée Mardi 2 mai - Nice Un univers à partir d’une feuille de papier Mercredi 3 mai - Sophia Antipolis Pour en savoir plus cliquez sur l'image
Le livret de parcours inclusif (LPI)
Le livret de parcours inclusif est une application qui propose des réponses pédagogiques aux besoins éducatifs particuliers des élèves, et ceci, avant la mise en œuvre ou dans le cadre de la mise en œuvre d’un programme personnalisé de réussite éducative (PPRE), d’un...
Lettre de rentrée 2022 : “mathématiques en BTS”
La lettre de rentrée de l’inspection générale de l’éducation, du sport et de la recherche de mathématiques fait notamment le point sur les rénovations de filières et l'évolution des modalités de certification. Pour la télécharger. ...
Définition de l’épreuve ou de la sous épreuve de physique chimie au brevet professionnel
La définition de l'épreuve ou de la sous épreuve de physique chimie au brevet professionnel de l'annexe III de l'arrêté du 3 mars 2016 est remplacée par l'annexe de l'arrêté du 5 octobre 2021 publié au JO du 16 octobre 2021. Les modifications concernent : les...
Modalités du Contrôle en Cours de Formation et programmes en vigueur en Bac. Pro et CAP
Document récapitulatif concernant les modalités du Contrôle en Cours de Formation et les programmes en vigueur dans les classes de CAP et de Bac. Pro. en mathématiques – physique-chimie. Le récapitulatif.
Le point sur les mathématiques dans les BTS à la rentrée 2021 de l’IGÉSR
Lettre de rentrée de l’inspection générale de mathématiques pour les BTS
Familles de métiers
De nouveaux guides pédagogiques d’accompagnement pour la mise en oeuvre des familles de métiers sont disponibles sur la page Éduscol Transformer le lycée professionnel : • Famille des métiers des transitions numérique et énergétique• Famille des métiers de la...
Dispositif d’accompagnement renforcé
Le groupe de travail académique "Accompagnement Renforcé" propose une infographie qui présente le dispositif d’accompagnement renforcé en classe de Terminale Bac Pro. En ce qui concerne, la préparation à la poursuite d'études : en mathématiques, un programme...
Activités pédagogiques réalisées dans le cadre des ateliers didactiques
Ces activités pédagogiques ont été réalisées dans le cadre des ateliers didactiques. Elles ont pour thème le module « Fonctions » du programme de seconde. Elles sont proposées non pas comme des modèles validés par le corps d’inspection, mais à titre d’exemples de ce...
Modalités de réalisation et d’évaluation du chef-d’œuvre en baccalauréat professionnel.
Une circulaire parue au bulletin officiel n° 41 du 29 octobre 2020 précise les modalités de réalisation et d’évaluation du chef-d’œuvre en baccalauréat professionnel. Pour consulter la circulaire Quelques éléments figurant dans la circulaire Le chef-d'œuvre est la...
Suppression du diplôme intermédiaire
Un décret paru au journal officiel du 23 octobre 2020 supprime dès cette année scolaire l’obligation qui incombait aux candidats à l’examen du baccalauréat professionnel, sous statut scolaire, de présenter en classe de première un diplôme de niveau 3 (CAP ou BEP). En...
Textes officiels : les nouveautés.
Bulletin officiel n°41 du 29 octobre 2020 Baccalauréat professionnel Modalités de l'évaluation du chef-d'œuvre prévue à l'examen du baccalauréat professionnel Arrêté du 20-10-2020 - JO du 22-10-2020 (NOR : MENE2019530A) Réalisation du chef-d'œuvre au baccalauréat...
Tests de positionnement
Les élèves de 1re année de CAP et de 2de professionnelle passent en début d’année des tests de positionnement afin d’identifier leurs acquis et leurs besoins en français et en mathématiques. Après les tests, seront disponibles : un bilan individuel de l’élève, une...
CAP et Bac. Pro. : programmes et rattachement des spécialités aux groupements
Les programmes pour le CAP et pour la seconde professionnelle sont définis par arrêté du 3 avril 2019 publiés au BO spécial n° 5 du 11 avril 2019. Pour la première et la terminale professionnelle ils sont défini par arrêté du 3 février 2020. Ils entrent en vigueur à...
Liste des connaissances et capacités effectivement traitées lors de l’année scolaire 2019-2020
Il serait utile qu’une liste des connaissances et capacités effectivement traitées par une classe lors de l’année scolaire 2019-2020, soit à la disposition du professeur prenant en charge cette même classe cette année scolaire. Cette liste permettrait en effet...
Modalités pratiques de la rentrée 2020 – Protocole sanitaire
L'objectif de cette rentrée 2020 est d'accueillir tous les élèves dans un cadre serein, propice aux apprentissages et à la reprise de la vie collective. Afin de garantir la protection des élèves et des personnels, la rentrée doit être assurée dans le respect des...
Nouvelle version des programmes du cycles 4
Publication au BO du 30 juillet d’une nouvelle version des programmes du cycle 4 afin de renforcer les enseignements relatifs au changement climatique, à la biodiversité et au développement durable.
Modalités des épreuves de baccalauréat professionnel à compter de la session 2022
L’arrêté définissant les modalités des épreuves de baccalauréat professionnel à compter de la session 2022 est paru au JO du 5 juillet 2020. Comme actuellement, les candidats ayant préparé le baccalauréat professionnel par la voie scolaire dans des établissements...
CoronaVirus : Continuité Pédagogique
Un espace d’échanges pour la mise en œuvre de la continuité pédagogique par les professeurs de mathématiques physique-chimie de l’académie de Nice est accessible sur Magistère: https://magistere.education.fr/ac-nice/course/view.php?id=8565§ion=1 ...
Circulaire relative aux modalités d’évaluation du chef d’œuvre
NOR : MENE2002480C Circulaire n° 2020-039 du 14-2-2020 MENJ - DGESCO A2-3 Texte adressé aux rectrices et recteurs d'académie ; aux vice-recteurs ; au directeur du Siec d'Île-de-France ; aux inspectrices et inspecteurs d'académie-directrices et directeurs académiques...
Programme de mathématiques de CAP : rattachement des spécialités de CAP aux groupements 1 et 2
Le rattachement des spécialités de CAP aux groupements 1 et 2 du nouveau programme de mathématiques a été publié sur le site Eduscol. Pour consulter le fichier (xls).
Programmes de mathématiques et de physique-chimie des classes de première et terminale professionnelles
Les programmes de mathématiques et de physique-chimie des classes de première et terminale professionnelles ont été publiés au bulletin officiel spécial n°1 du 6 février 2020. Ces programmes entrent en vigueur à la rentrée de l’année scolaire 2020-2021 en classe de...
Arrêté du 28 novembre 2019 définissant les modalités d’évaluation du chef-d’œuvre prévue à l’examen du CAP
L’arrêté du 28 novembre 2019 définit les modalités d’évaluation du chef-d’œuvre prévue à l’examen du certificat d’aptitude professionnelle. Il est consultable sur le site Légifrance. Ces modalités diffèrent selon que l’établissement ou le centre de formation...
Exploitation pédagogique du test de positionnement en mathématiques à l’entrée en seconde professionnelle.
Ce document explicite une méthodologie possible pour réaliser une analyse didactique des items du test de positionnement en mathématiques à l’entrée en seconde professionnelle que la DEPP a libérés. Cette analyse vise à aider les enseignants, à partir d’une...
Utilisation de la calculatrice aux examens pour la session 2020
À compter de la session 2020, la circulaire n° 2015-178 du 1er octobre 2015 relative à l'utilisation des calculatrices électroniques aux examens et concours de l'enseignement scolaire (baccalauréat, DNB, CAP, BEP, concours général....) est mise en œuvre. Cette...
Nouveautés pour les BTS à la rentrée 2019
Note de l’Inspection générale de l’éducation, du sport et de la recherche concernant les programmes et la certification à la rentrée 2019 en BTS. BTS_math_rentrée_2019 (pdf) La note est accompagnée d’un tableau récapitulatif des différentes spécialités de BTS et des...
Lettre Édu_Num Mathématiques N°31
Sommaire ZOOM SUR Bac 2021 Les repères de progressivité ÉVÉNEMENTS Ouverture de l'année des mathématiques ENSEIGNER AVEC LE NUMÉRIQUE Prim à bord Banque de ressources numériques pour l'École Édu-Up Mathscope Le portail AJN SE TENIR INFORMÉ Twitter éduscol Maths...
Ressources pour la mise en œuvre des nouveaux programmes
Éduscol propose pour la mise en œuvre des nouveaux programmes des classes préparatoires au CAP et au baccalauréat professionnel : quatre exemples d'activités en physique-chimie : Déploiement automatique de stores (CAP), Déploiement automatique de store (seconde),...
Lettre de rentrée de l’année scolaire 2019 / 2020
Lettre de la rentrée 219 à destination de l’ensemble des collègues de mathématiques physique-chimie de l'académie de Nice de la part des IEN.
NOUVELLES MODALITÉS D’ÉVALUATION EN CAP
Elles sont définies par l’arrêté du 30 août 2019 fixant les unités générales du CAP et définissant les modalités d’évaluation des épreuves d’enseignement général. Les candidats ayant préparé le CAP par la voie scolaire dans des établissements d’enseignement public ou...
La transformation du lycée professionnel : outils et ressources pour la mise en œuvre
RESSOURCES D’ACCOMPAGNEMENT DE LA TRANSFORMATION DE LA VOIE PROFESSIONNELLE Des ressources d’accompagnement des nouveaux programmes sont en cours de finalisation ; elles seront progressivement mises en ligne sur le site éduscol ; elles concerneront notamment...
Arrêté du 19 avril 2019 portant application des nouvelles organisations d’enseignements dispensés dans les formations sous statut scolaire préparant au Bac. Pro. et au CAP
Pour chaque spécialité de baccalauréat professionnel existant à la date de l’arrêté, il est précisé : le secteur dont elle relève pour l’application de l’annexe 2 de l’arrêté du 21 novembre 2018 susvisé ; les enseignements au choix, économie-gestion ou économie-droit...
Lettre Édu_Num Physique-chimie N°29
Lettre Édu_Num Physique-chimie N°29 Mai 2019 Sommaire 1. ZOOM SUR DES RESSOURCES POUR SE FORMER AUX NOUVEAUTÉS DU PROGRAMME DE LGT A. Des tutoriels vidéos pour se former au langage Python et aux cartes à microcontrôleur B. Des ressources pour poursuivre la formation...
Grille horaire de la classe de troisième dite « prépa-métiers » au JO n°92 du 18 avril 2019
À la rentrée 2019, la classe de 3eprépa-métiers succèdera à la classe de 3eprépa-pro. Le journal officiel du 18 avril 2019 publie l’organisation horaire de la classe de 3eprépa-métiers. Cette classe a pour objectif de faire découvrir à des élèves volontaires un...
Publication des programmes de mathématiques et de physique-chimie de seconde professionnelle et de CAP
Les programmes de mathématiques et de physique-chimie de la classe de seconde professionnelle et des classes préparatoires au certificat d’aptitude professionnelle (CAP) ont été publiés au bulletin officiel spécial n° 5 du 11 avril 2019. Programme d'enseignement de...
Risques et sécurité en physique-chimie
Brochure qui apporte des éléments sur la prévention des risques dans des activités où des élèves et personnels peuvent être confrontés aux : – risques optiques ; – risques électriques ; – risques liés aux conditions de pression et de température. Pour consulter la...
Lettre Édu_Num Maths N°30 – Février 2019
Sommaire ZOOM SUR... Description de la plateforme Rechercher dans la base Proposer des ressources ENSEIGNER AVEC LE NUMÉRIQUE Pour le cycle 4 Académie de Corse - Fiche n°15247 Algorithmique débranchée au cycle 4 Trois activités débranchées autour de l'algorithmique....
Consultation sur les projets de programmes de mathématiques et physique-chimie pour la rentrée 2019
Les projets de programmes remis au ministre par le Conseil supérieur des programmes (CSP) font l’objet d’une consultation nationale du 18 février au 3 mars 2019. Cette consultation doit notamment permettre d’interroger :· l’approche générale des programmes...
Brevet Professionnel : proposition de sujets de mathématiques et de physique chimie pour illustrer les épreuves.
Depuis la session 2018, les modalités d’évaluation des épreuves de mathématiques et de physique-chimie des BP ont été modifiées. Des sujets de mathématiques et de physique-chimie sont proposés pour illustrer différentes configurations des activités prévues par le...
Desmos, une calculatrice graphique en ligne
Desmos est une calculatrice graphique en ligne disponible en version WebApp et en version application mobile. L'édition graphique se veut très visuel et réactive, sous une ergonomie simplifiée. Desmos permet de saisir des fonctions, de les visualiser, d'éditer les...
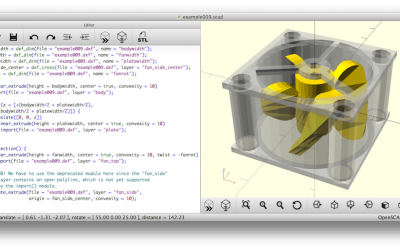
OpenSCAD, un logiciel permettant de créer des modèles de CAO 3D solides
OpenSCAD est un logiciel permettant de créer des modèles de CAO 3D solides. C'est un logiciel libre et disponible pour Linux / UNIX, Windows et Mac OS X. Contrairement à la plupart des logiciels libres pour créer des modèles 3D (tels que Blender), il ne se concentre...
La lettre Édu_Num Physique-chimie
En collaboration avec l'inspection générale de l'Éducation nationale et les Délégués académiques numériques (DAN), le bureau des usages numériques et des ressources pédagogiques propose l'envoi de lettres d'information autour du numérique dans les pratiques...
Lettre d’information Édu_Num Mathématiques
La lettre Édu_Num Mathématiques est une lettre d’information sur les usages, les ressources et les actualités de la discipline autour du numérique dans les pratiques pédagogiques. Réalisée en collaboration avec l’IGEN, elle a pour fonction de vous proposer des pistes...
A propos du site…
Depuis la rentrée 2018, le site PLPMS de l'académie de Nice est accessible depuis une nouvelle adresse : www.pedagogie.ac-nice.fr/plpms Cette nouvelle adresse sera suivie d'une mise à jour du site progressive. Un nouvel outil a été mis en place pour permettre de...
[CME1] Le salage des routes
Pourquoi le sel que l'on met sur la route fait-il fondre le verglas ? Dès que la température extérieure tombe au dessous de zéro degrés Celsius, la pluie se transforme en neige et l’eau sur la chaussée devient de la glace. Cette température est appelée est le point de...
Statistiques à 2 variables : troubles musculosquelettiques – TMS
En direct des ateliers : Une entreprise de BTP, très soucieuse de la santé de ses ouvriers, décide de publier quelques chiffres, pour une année des troubles musculosquelettiques (TMS). Public concerné : Elèves de terminale baccalauréat professionnel. Objectifs...
[SL3] Fibre optique à domicile
En direct des ateliers : Faire un lien entre les sciences et la vie courante par des notions que les élèves ont ou auront à manipuler en tant que citoyen utilisateur de nouvelles technologies. Publics concernés : Elèves d’une classe de terminale, 3ème année du...
Prix Perrin de Brichambaut 2017 – Les meilleurs projets sur les thèmes “METEO & CLIMAT”
Météo et Climat organise chaque année le prix Perrin de Brichambaut, avec le soutien de Météo-France. Ce concours national a été créé en 1997 afin d'honorer la mémoire de Christian Perrin de Brichambaut (1928-1995), ancien ingénieur à Météo-France et ancien président...
Les professeurs de 3PEP se réunissent pour “Scratcher” ensemble
Le mardi 6 décembre, pour les Alpes-Maritimes, et le jeudi 8 décembre, pour le Var, les professeurs de maths-sciences des classes de 3ème Préparatoire à l'Enseignement Professionnel se sont réunis pour une journée de formation consacrée à une des particularités du...